In this tutorial, we are going to learn about bubble sort and its implementation in detail.

Bubble Sort

• In-place algorithm.
• O(n^2) time complexity - Quadratic.
• It will take 100 steps to sort 10 items, 10000 steps to sort 100 items and 1000000 steps to sort 1000 items.
• Algorithm’s performance degrades quickly as the number of items you need to sort grows, but it’s a commonly taught algorithm.

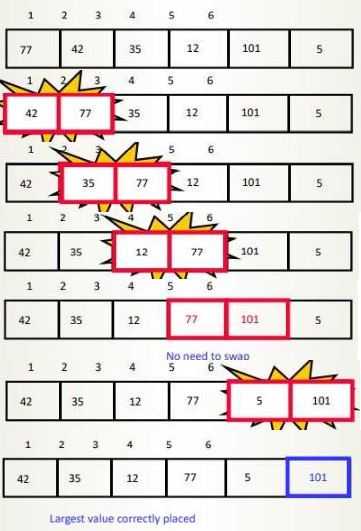
“Bubbling Up” the Largest Element

• Traverse a collection of elements.

  • Move from the front to the end
  • “Bubble” the largest value to the end using pair-wise comparisons and swapping.

Bubble Sort Algorithm

Bubble (DATA, N)

1. Repeat Step 2 and 3 for K=1 to N-1.
2. [Initialize Pass Pointer P] Set P=1.

3. [Execute Pass] Repeat while P <= N-K.

   1. if DATA [P] > DATA [P+1], then:
      Swap DATA [P] and DATA[P+1]
      [End of if Structure.]
   2. Set P = P+1.
      [End of Inner Loop.]
      [End of Step1 Outer Loop.]
4. Exit

Bubble Sort Programmatic Implementation in Java

public class BubbleSort {
    public static void main(String[] args) {
        int[] intArray = {  77, 42, 35, 12, 101, 5 };
        for (int lastUnsortedIndex = intArray.length - 1; lastUnsortedIndex > 0;
                lastUnsortedIndex--) {
            for (int i = 0; i < lastUnsortedIndex; i++) {
                if (intArray[i] > intArray[i + 1]) {
                    swap(intArray, i, i + 1);
                }}}

        for (int i = 0; i < intArray.length; i++) {
            System.out.print(intArray[i] + " ");
        }}
    public static void swap(int[] array, int i, int j) {
        if (i == j) {
            return;
        }
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }}

Output:

5 12 35 42 77 101