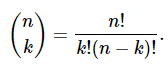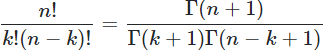In this tutorial we are going to see about performing arbitrary-precision computation and much more math (and fast too) than what is possible with the built-in math library in Python.

Limitless math?

Sounds like a catchy title? Well, what we really meant by that term is arbitrary-precision computation i.e. breaking away from the restriction of 32-bit or 64-bit arithmetic that we are normally familiar with.

Here is a quick example.

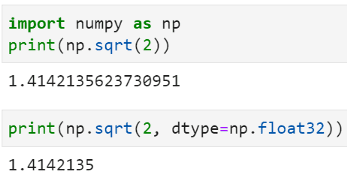
This is what you will get as the value for the square-root of 2 if you just import from the standard math module of Python.

You can use Numpy to choose if you want the result to be 32-bit or 64-bit floating-point number.

But what if you wanted the result up to 25 decimal places…

1.414213562373095048801689

Or, 50 decimal places?

1.4142135623730950488016887242096980785696718753769

How are we getting these results?

Just by using a neat little package called mpmath. Let’s examine it in detail.

Arbitrary-precision computation with mpmath

Mpmath is a Python library for arbitrary-precision floating-point arithmetic. For general information about mpmath, see the project website.

From its website, apart from arbitrary-precision arithmetic, “mpmath provides extensive support for transcendental functions, evaluation of sums, integrals, limits, roots, and so on”. It also does many standard mathematical tasks like,

• Polynomials
• Root-finding and optimization
• Sums, products, limits, and extrapolation
• Differentiation
• Numerical integration (quadrature)
• Solving ordinary differential equations
• Function approximation
• Numerical inverse Laplace transform.

In short, it’s a power-packed math library with limitless possibilities! We will explore some of the features in this article.

Installing and choosing a fast backend engine

Just pip.

pip install mpmath

By default, mpmath uses Python integers internally. If gmpy version 1.03 or later is installed in the system, mpmath will automatically detect it and use gmpy integers w/o any change to the high-level user experience. Using this backend makes its operations much faster, especially at high precision.

gmpy2 is a C-coded Python extension module that supports multiple-precision arithmetic. Here is how to install it.

Choosing Precision

There is a whole lot of material about choosing and controlling precision with mpmath. Readers are encouraged to consult this reference directly. I am just going to show you the quick way to set precision as you work along.

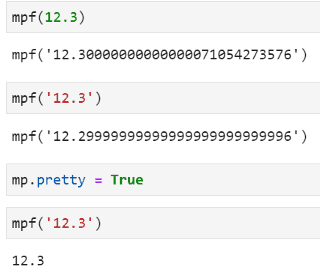
Use mpf instances instead of regular float

In the code snippets above you might have noticed a function mpf. An mpf instance holds a real-valued floating-point number. They work analogously to Python floats, but support arbitrary-precision arithmetic.

You should define mpf using strings (and not Python floats) as arguments to get true accuracy. You can also set mp.pretty to True for rounding w/o losing the internal accuracy.

Now some magic! Factorial calculation 11,000 times faster

The mpmath can do large calculations using smart tricks whenever applicable. One example is factorial. For large numbers, it can use approximations appropriately without being instructed and give us the result much faster than the default Python math module.

Here is what happens when we attempt to calculate the factorial of 100,000. mpmath is 11,333X faster.

Rational and complex numbers are native citizens

We can throw in rational or complex numbers as easily as floating-point numbers into the mix. For this, we need to use a magic function mpmathify which works with sympy internals to interpret those quantities.

We don’t have to import Python modules like fraction or cmath to work with such quantities at a precision of our choice.

Learn about all other general utility functions that mpmath offers.

Quick plotting

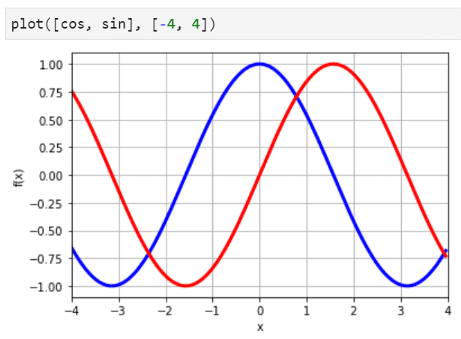
If Matplotlib is available on the system, mpmath offers a fast and easy plotting choice just by passing a list of functions and the corresponding ranges.

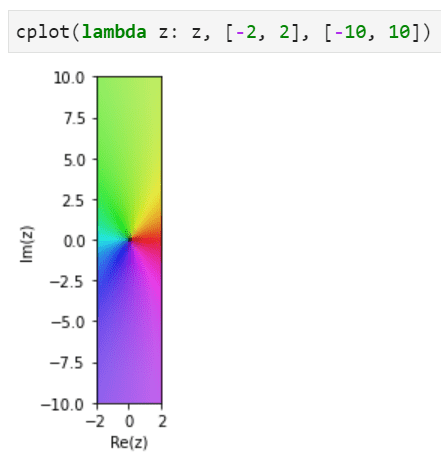
Here is a single-line code example,

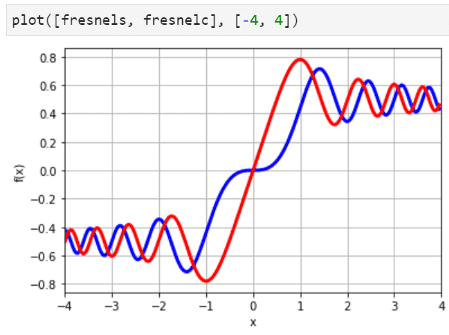
Another example with Fresnel functions,

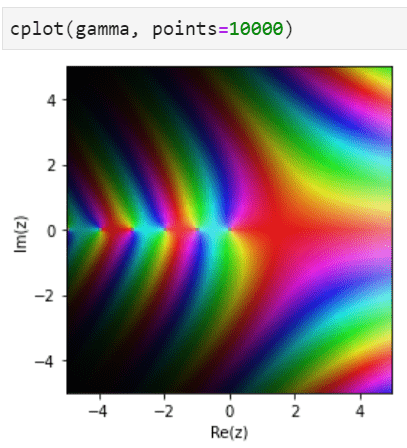
Complex quantities can be plotted as easily with cplot. By default, the complex argument (phase) is shown as color (hue) and the magnitude is shown as brightness.

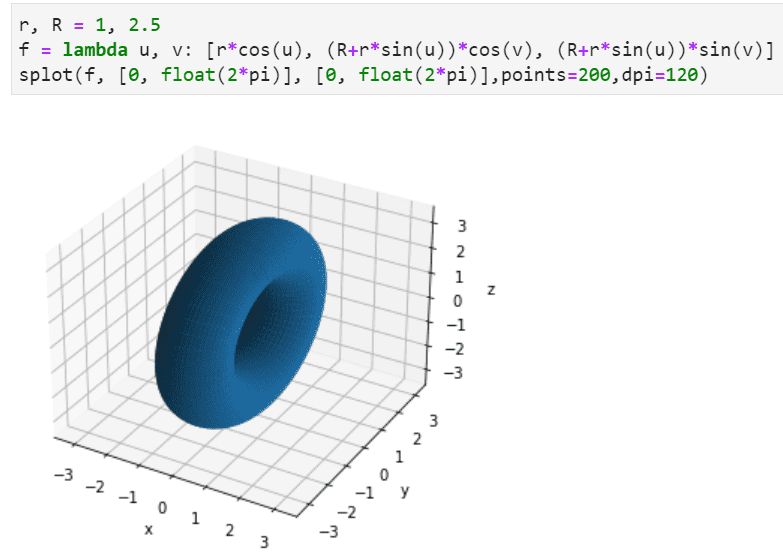
Surface plots are also game,

Special functions

mpmath supports hundreds of special functions out-of-the-box. Here is a partial screenshot of that list. Refer to this documentation for details.

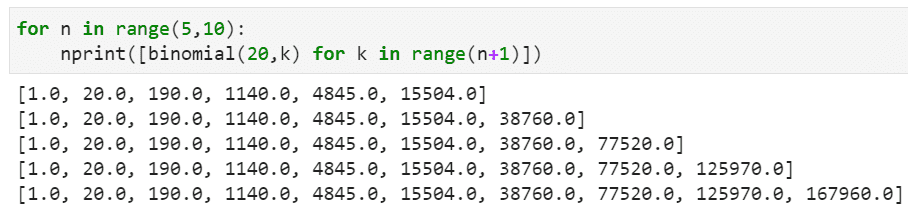
Binomial coefficients

Fast and easy computation of binomial coefficients for statistics and combinatorial math with binomial function,

This function supports massively large arguments, which is where this really shines. Scipy calculation is faster but for large numbers, Scipy does not even run!

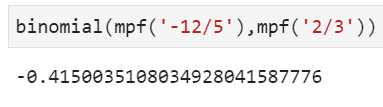
And, extensions to non-integers and negative arguments are natural (using Gamma function),

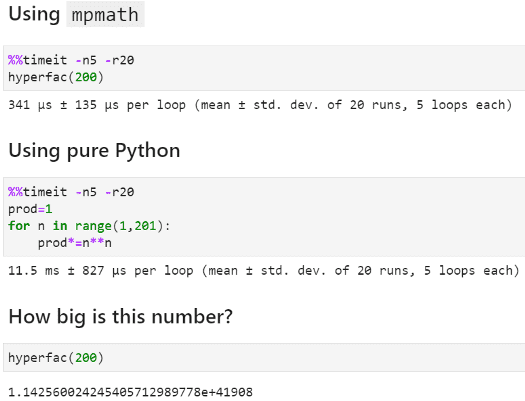
Hyperfactorials

For integers, hyperfactorials are defined as,

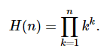
They are really large. Can you think of an easy way to calculate this kind of number?

Fibonacci number

Calculating the Fibonacci sequence with naive Python (recursive function) is a popular interview question because it can be done in a few different ways which differ dramatically in efficiencies.

However, calculating approximate solutions with large arguments or non-integer (even complex) arguments is natural and easy for mpmath. This is not so straightforward to achieve using native Python coding.

Polynomial evaluation and roots

Easy and fast evaluation of polynomials of any order and root finding using polyeval and polyroots functions. Of course, polyroots evaluates all real and complex roots at one go.

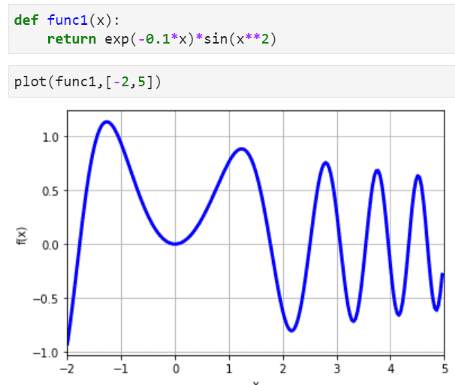
Root-finding of arbitrary functions

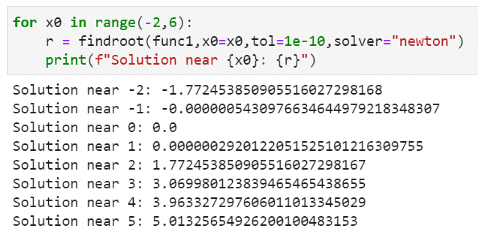
We can use the rootfind function to search for roots of any arbitrary function. Here is an example,

Then, we look for solutions near all the integers from -2 to 5 and it finds multiple solutions corresponding to all the values of x at which the function crosses zero.

Numerical calculus

Evaluate derivatives of any order and any function,

Partial derivatives are easy,

Look at this reference to see other advanced examples and functions related to derivatives.

1-D integrals

Simple and fast evaluation to arbitrary precision,

2-D or 3-D integrals

Two- or three-dimensional integrals are also game!

Ordinary differential equation

We can use odefun to solve for ordinary differential equations with known boundary conditions.

Or, a more difficult one,

Matrix and linear algebra

The mpmath package also offers all the standard operations involving matrices and linear algebra. For brevity, we just refer to the documentation here instead of showing examples.

Summary

In this article, we showed a powerful Python library and its capabilities for performing arbitrary-precision numerical computation involving all kinds of numbers and functions. Basically, the main advantage of this library is that it covers a very large swath of mathematical domains (algebraic, number-theory, calculus, special functions, etc.) and everything is available under a single roof without loading multiple libraries.

Many of the usages of this library are in complex scientific/ technological domains such as finite-element simulations or cryptography, but as a number-enthusiast, you can always pick up useful functions from this package whenever you need for your data science or machine learning work.