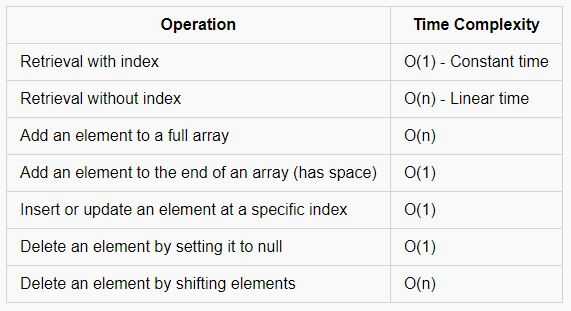
What is the Big-O notations of the Array operations
In this tutorial, we are going to learn about the different Big-O notations for Array operations like insertion, deletion, sorting etc.
Firstly, lets see about retrieval of elements from an array.
- Multiply the size of the elements by its index.
- Get the start address of the array.
- Add the start address to the result of the multiplication.
For an int array, assume element starts at the address 12. each int is 4 bytes.
To retrieve intArray[0] = 12 + 0 *4 = 12
To retrieve intArray[1] = 12 + 1 *4 = 16
To retrieve intArray[2] = 12 + 2 *4 = 20
To retrieve intArray[3] = 12 + 3 *4 = 24
To retrieve intArray[4] = 12 + 4 *4 = 28
Here is the example, To retrieve the element from array without knowing its index. Let’s say we want to find the element 55.
- No matter how many elements are in the array. It takes the above three steps only to retrieve the element.
- If no of elements is equal to n, the steps to retrieve never changes and this is known as constant time complexity that is designated by O(1) which means that even the number of elements increases algorithm’s performance doesn’t change.
-
So the retrieval of an element in an array can be done in O(1) if index is known.
public class ArrayOperations { public static void main(String[] args) { int[] intArray = new int[7]; intArray[0] = 20; intArray[1] = 35; intArray[2] = -15; intArray[3] = 7; intArray[4] = 55; intArray[5] = 1; intArray[6] = -22; int index = -1; for (int i = 0; i < intArray.length; i++) { if (intArray[i] == 55) { index = i; break; } } System.out.println("index = " + index); } }Output:
index = 4Well, the worst case would be that 55 is in the last position in the array and so the worst case is that we had to search the entire array before we found 55.
Now there are seven items in the array. so n equals to seven for this example and that means we would have to looped n times.
- In this situation, the number of elements does influence how many steps we’re gonna have to perform Because if we have 100 items in the array, then in the worst case we’re gonna have to loop 100 times.
- If we have a thousand items in the array, in the worst case loop runs for a thousand times.
- If we have a million items in the array and worst case is loop runs a million times.
- So this looks like linear time complexity because when n is one, we have to loop once and when n is 10, we have to loop 10 times and so on and it is progressing in a linear manner.
- So in retrieval, when we know the index, we can do that in O(1) and when we do not know the index it is O(n) because we have to find the element first and in the worst case, we’d have to traverse or loop over the entire array.